Virtue - An Inherently Parallel Programming Language

Throughout centuries of the development of computing equipment serial processing was more or less the only option, therefore, after the event of modern day computing, from the first half of the 20^th century, and the development of programming languages, most of the computer-linguistical effort was put into the development of conventional serial programming languages. And, to cite John Backus from his ACM paper (ref. 5) of 1978(!): "Programming languages appear to be in trouble. Each successive language incorporates, with a little cleaning up, all the features of its predecessors plus a few more." "Each new language claims new and fashionable features, such as strong typing or structured control statements, but the plain fact is that few languages make programming sufficiently cheaper or more reliable to justify the cost of producing and learning to use them." "For twenty years programming languages have been steadily progressing toward their present condition of obesity; as a result, the study and invention of programming languages has lost much of its excitement." Well, now it is already 50 years, and much more so than in 1978 most of the programming is done in "conventional", von-Neumann style languages.

However, as now at the begining of the 21^st century computing necessities have grown enormously and the speedup of individual processing elements, primarily serial processing units, has stopped, computer experts (and computer linguists specifically) have to, finally, start rethinking the basic principles of programming in terms of parallelism, as the only viable option is the (already starting) development of multi-processor (SMP or other), multi-computer (cluster) or multi-cluster (grid) data processing systems. This development will lead towards future operating systems based on “device distributed intelligence”, i.e. more and more specifical functions (like graphics, print-out processing, random number generation etc.) will be assigned to special processing elements, which often (as in graphics) employ inherently parallel algorithms.

Somehow, what seems that computer users, and programmers like, would like to have as computing equipment is what can be seen in many Science Fiction novels and films, and to the large audience very known through the Star Trek series – computers which can be reprogrammed in several minutes (or several hours in a case of a heavy problem), computers which can say in advance how long a specific data search or computation will take, computers which are largely self repairing, and a human interface which is logical, simple and powerful, either using touch-screen or voice communication. Actually, what we strife towards is the jump from Morse-code telegraphs towards telephones. This means that you do not any more need a specialist who knows the Morse-code, but only somebody who knows how to build, maintain and repair the telephone.

An investigation in basic principles of computer programming, as well as the principles by which we serialize the inherently extremely massively parallel universe around us into serial algorithms, was performed, and a new(ish) approach taken.

One of the major points which started being obvious during the investigation of the programming principles is that most (or almost all commonly used) computer languages, being primarily serially oriented both in their semantics and in their syntax – i.e. in their whole grammar, enforce the decontextualisation of their data structures mostly in their imperative parts. In other words this means that though a complex data structure may be declared in the language, the operations on that data structure are linguistically restricted on individual data elements from that data structure. As a consequence of this approach the context of the individual data elements in a data structure has been erased from the programme, leading to important information loss, and the language executor (compiler, interpreter, assembler…) has theoretically¹ no possibility to ‘know’ that the user is actually doing parallel processing in a serial way.

Interestingly enough, although obviously a consequence of the above-mentioned centuries of serial computing², there are not many computer languages at all which do not do this ‘decontextualisation’ of their data structure operations – notably between these are APL and APL-children (APL2, J, K, A+…), and the ‘array processing’ linguistical branch. Unfortunately, of those few languages which keep the operations context available for the executing processor and therefore allow the processor (usually an interpreter, not the low level processing units) to make intelligent decisions on the automatic parallelisation of each particular operation on (possibly) different data structures³ there is presently (2007) no publicly (particularly open-source) available parallel implementations. Many so-called parallel programming languages actually necessitate explicit programmer description of the parallelistic execution, as well as (for example in Occam) explicit inter-serial-part-of-the-parallel-algorithm communication.

Based on the above, the approach was taken to define a new data processing language, or better to say a new data processing language family, which would allow reasonably simple algorithm description for complex data structures, and which would allow the lowest level “processor” to automatically distribute (parallelise) the operations execution on a set of processing units. Generally the idea is to have a hierarchy of languages, whereas the lowest level one, described on these pages, has to be as close to the computer hardware level as possible, given the imposed complexity, and should actually behave as a Virtual Executor. The job of the Virtual Executor is to do all the necessary execution and parallelisation during execution based on the data, i.e. data types and data structures. Therefore it could be said that the resulting Virtual Executor is parallely programme and data structure driven.

The result of this approach is the first version of Virtue – a very "low level" (actually Reversed Polish Notation stack based non-von Neumann language and its processor) “processor” was developed. The Virtue language is “low level” in the sense that it is actually based on the principles of an autocoding language (each word of the language is an individual instruction to the “processor”) and even not an assembly language.

However, Virtue has complex data structures (scalars, arrays of any dimension, array elements which are themselves structures of scalars or arrays…) and diverse data types (booleans; fuzzy logicals; characters; numbers – real, complex, quaternion, octonion; addresses; functions; labels or specific types like planetary ephemeris, pixels etc.). The inclusion of e.g. fu nctions as data types, intermixable with any other datatype, as well as the form in which the programme itself is internally represented - in the exactly same way as contents of a variable, enables Virtue to use, for example, variable functions whenever necessary, or to define function parallelism (e.g. by applying a vector of functions to a vector of values - which may be 'passive' functions by themselves)⁴.

Virtue has an almost fully orthogonal approach towards data – any operation that has sense is (hopefully also in the implementation) usable. However, nonsensical operations (like e.g. square root of a character) are strictly disallowed. The execution framework of Virtue is very forgiving, yet strict, in imposing the processing rules for different combinations of data structures and data types.⁵

Documentation and Implementation

A (preliminary) Virtue 0.7 langaugage manual: The Virtue of Programming in Virtue is available. It represents for the most part the newest version of Virtue.

Presently Virtue is available for executable download as Virtue 0.8 (still in development, more words and constructions will be included over time).

Please use Virtue 0.3 executables if available! Virtue 0.2 is not supported any more.

Scientific Visualisation Using Virtue

Virtue is used in the VEPPAR Scientific Visualisation Project. The following are two visualisations calculated by Virtue and rendered by Povray:

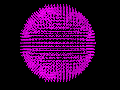
A rendering of a fourdimensional (discrete points) sphere (the fourth dimension is represented by the cones).

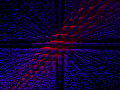
A rendering of the magnetic field around the conductor, where the colour and "point" size represent the field strength at that point - red center is the magnetic field around the conductor itself. The Magfield Virtue programme calculates the magnetic field in discrete points and prepares its results for direct feed as a Povray programme, which was then executed on the Grid. The first part of the Virtue programme, the 'ARGS 3 FUNCTION' '.Magfield' calculates the magnetic field around the conductor (a 3-D line going diagonally throught the render space - function '.line3'). Finally, the last part of the Virtue programme prints out the proper Povray programme, converting the '.Magfield' result data into appropriate arguments as parts of Povray language sentences.

1Practically it is possible to automatically regain a certain knowledge on the data element context in specific cases, as e.g. when a loop transiting an array has a fixed number of iterations – based on pre-execution knowledge (by the programmer) of e.g. how many elements are in the processed data structure. There are certain “parallelizing” compilers on the market for several much used languages, but they can do the “parallelisation” of the algorithm described in a serial language only for very special cases. Theoretically, the lost context information is not regainable.

2It is probably important to mention that between humans, e.g. in mathematics, the algorithms (as for example mathematical formulas) are described in a contextfull way, however, due to our own restrictions, we always calculate the results stepwise, usually completing as much as possible work on one element of an array before proceeding to the next, which is usually by applying the given formula completely on individual data points. This inherently human approach may have also lead to the adoption of strictly serial programming languages in the past.

Parallel programming mindframe, on the other hand, starts with the same contextfull algorithm (e.g. formula), but, as opposed to the serial mindframe, executes not the whole formula on the first data structure element, and then again on the next, but executes the first operation from the formula on each data element of the structure (e.g. array) before proceeding to the next operation from the formula.

3This is, naturally, dependent on a particular language implementation, although it is ‘automatical’ due to the fact that the actual execution parallelisation has to be developed by the language implementor, and the “programmer” does not have to think at all about how much and which of her (or his) algorithm is executed in parallel, and on how many computing resources.

4The present day implementation of Virtue (Virtue 0.2 / Virtue 0.3) does not fully support all the structural Virtue instructions and all of the mentioned data types. This has to be taken into account if using Virtue 0.2 / Virtue 0.3.

5For example, a dyadic (two argument) operation on arrays whose dimensions are not equal is prohibited, except if one of the argument array dimensions is a subset of the other argument’s array dimensions, or one of the arguments is a scalar.

by Zorislav Shoyat

Documentation and Implementation

Scientific Visualisation Using Virtue